[MachineLearning] K最邻近算法

What is the KNN

KNN,全称K Nearest Neighbor.

K最临近算法是机器学习中一个比较经典的算法.主要用来分类.

用一张Wikipedia的图例展示KNN:

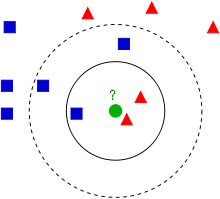
图中已知两类:红色三角形和蓝色矩形的分布,现在图中心有一个未知的类别,如果要将其归类,它应该是哪一类?(请不要说绿色圆形…)

使用KNN算法:

• k=3,选取离其最近的3个点:两个红色一个蓝色.选取其中出现最多的红色三角,推断中心也是一个红色三角形.
• k=5,选取离其最近的5个点:两个红色三个蓝色.根据周围的类别比例,推断中心是蓝色矩形.

这就是KNN算法,一个基于一种数据统计的方法.这里的K是选取附近的点的个数.通过计算方式可以知道,K必须取奇数,避免平票的情况.

可以理解为,KNN是由待分类数据由其附近的数据投票决定其类别.

How to use KNN

拿西瓜书上面一些数据举个例子:

密度	含糖率	好瓜
0.774	0.376	是
0.697	0.460	是
0.666	0.091	否
0.243	0.267	否

问:如果现在有一个瓜的密度:0.657,含糖率:0.198,那么它是好瓜吗?

用KNN计算:

密度	含糖率	距离	K=1	K=3
0.774	0.376	$(0.774-0.657)^{2}$+$(0.376-0.198)^{2}$=0.045373	不投票	是
0.697	0.460	$(0.697-0.657)^{2}$+$(0.460-0.198)^{2}$=0.070244	不投票	是
0.666	0.091	$(0.666-0.657)^{2}$+$(0.091-0.198)^{2}$=0.01153	否	否
0.243	0.267	$(0.243-0.657)^{2}$+$(0.267-0.198)^{2}$=0.176157	不投票	不投票

通过计算距离,可以知道:

• K=1,不是好瓜
• K=3,是好瓜

其实,通过含糖率数据可以知道,预测的这个瓜不是好瓜.

所以通过这个结果可以看到,最终预测的准确性和K的数量关系不大.比较关键的是选取判断属性,如果选取含糖率计算的话,准确率会变好.

上面并不是一个严谨的推论,但可以看出,面对线性变化的某些属性,用KNN还是有一些准确性的.也正因此,KNN还可以做一些插值操作,可以平滑曲线.

L1 & L2 distance

• L1 distance:

  $$d_{1}(I_{1}, I_{2})=\sum_{p}|I_{1}^{p} - I_{2}^{p}|$$

• L2 distance:

  $$d_{2}(I_{1}, I_{2}) = \sqrt{\sum_p(I_{1}^{p} - I_{2}^{p})^2}$$

http://blog.csdn.net/zhangxb35/article/details/55223825

http://blog.csdn.net/kangroger/article/details/52338344

http://cs231n.github.io/classification/